1. Introduction

When using impaction samplers, it is also necessary to correct for impact coincidence error using a positive-hole correction factor. This occurs because it is possible for multiple particles, each containing one or more organisms, to pass through a particular jet hole during sampling and impact onto agar media plate, with one or more colonies forming at the same impaction sites.

The colonies formed by the multiple impacted particles can then be inaccurately counted as a single colony. As the number of organism-containing particles impacted onto the growth medium increases, the probability that the next organism-containing particle will impact an "occupied" hole increases. For example, if 75% of the holes have received at least one particle, the chance that the next particle will impact a "clean" hole is one in four (25%).

2. Numerical Coincidence Correction

To account for this, a probability-based coincidence correction factor needs to be applied to the counted colonies. The basic formula for coincidence correction is as follows:

(1)

The limitation of the model is reached when the observable count reaches the number of jet holes in the sieve impaction head. The last term in the number sequence will cause a divide by zero at Cp = N+1.

2.1. MATLAB Model

The following MATLAB model will produce count corrections using the above coincidence correction.

C_p   = 100   % the number of colonies counted on the media/culture plate
N     = 220   % Holes in sieve impaction sampling head
C_ecp = 0;    % the estimated culturable particle colonies 

for i=0 : 1 : C_p-1
    C_ecp = C_ecp + N/(N-i);
end
C_ecp = C_ecp + N / (N-C_p+1);
C_ecp = round(C_ecp)

3. Simplified Macher Method

Studies by Macher J.A Am Ind Hyg Assoc J. 1989 Nov;50(11):561-8, have shown the correction of colonies, using the parameter notation above, can be given by:

(2)

This simplified method does not require computer based modelling to produce a result. If the count exceeds the number of holes, N, by more than 5% then equation(2)will fail and the results cannot be trusted, and include an imaginary component. The plot below illustrates the results, with the imaginary component ignored (Modelled using MATLAB).

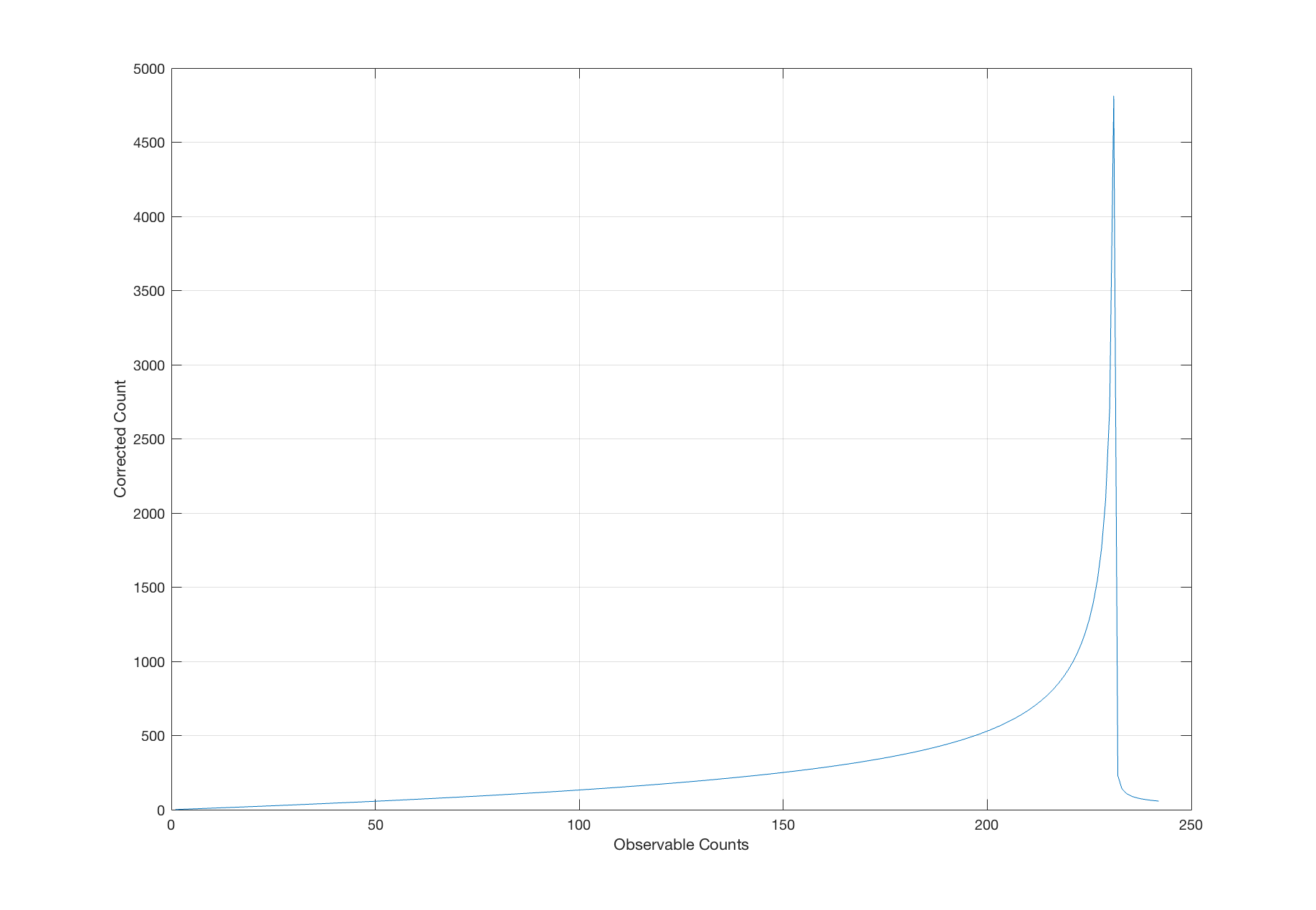
Macher equation failing at counts beyond sampling head holes.

4. Comparison

The following MATLAB model plots a comparison of the coincidence correction numerical method(1)versus the simplified Macher equation(2) for a 220 hole sampling head with ‘observable’ counts from 0 to 220.

N   = 220   % Holes in sieve impaction sampling head
Cns = zeros;
Cmc = zeros;
Cc  = zeros;

for x=1 : 1 : N   % counted colonies
    Cc(x) = x;

    % Numerical Coincidence Correction Model
    C_ecp = 0;    
    for i=0 : 1 : Cc(x)-1
        C_ecp = C_ecp + N/(N-i);
    end
    C_ecp = C_ecp + N / (N-Cc(x)+1);
    Cns(x) = floor(C_ecp);

    % Macher simplified model
    Cmc(x) = x* ( 1.075/(1.052-(Cc(x)/N)) )^0.483;
end

plot( Cc, Cns, Cc,Cmc )
grid on
legend('Coincidence Numerical Correction','Macher Simplification')
xlabel('Observable Counts')
ylabel('Corrected Count')

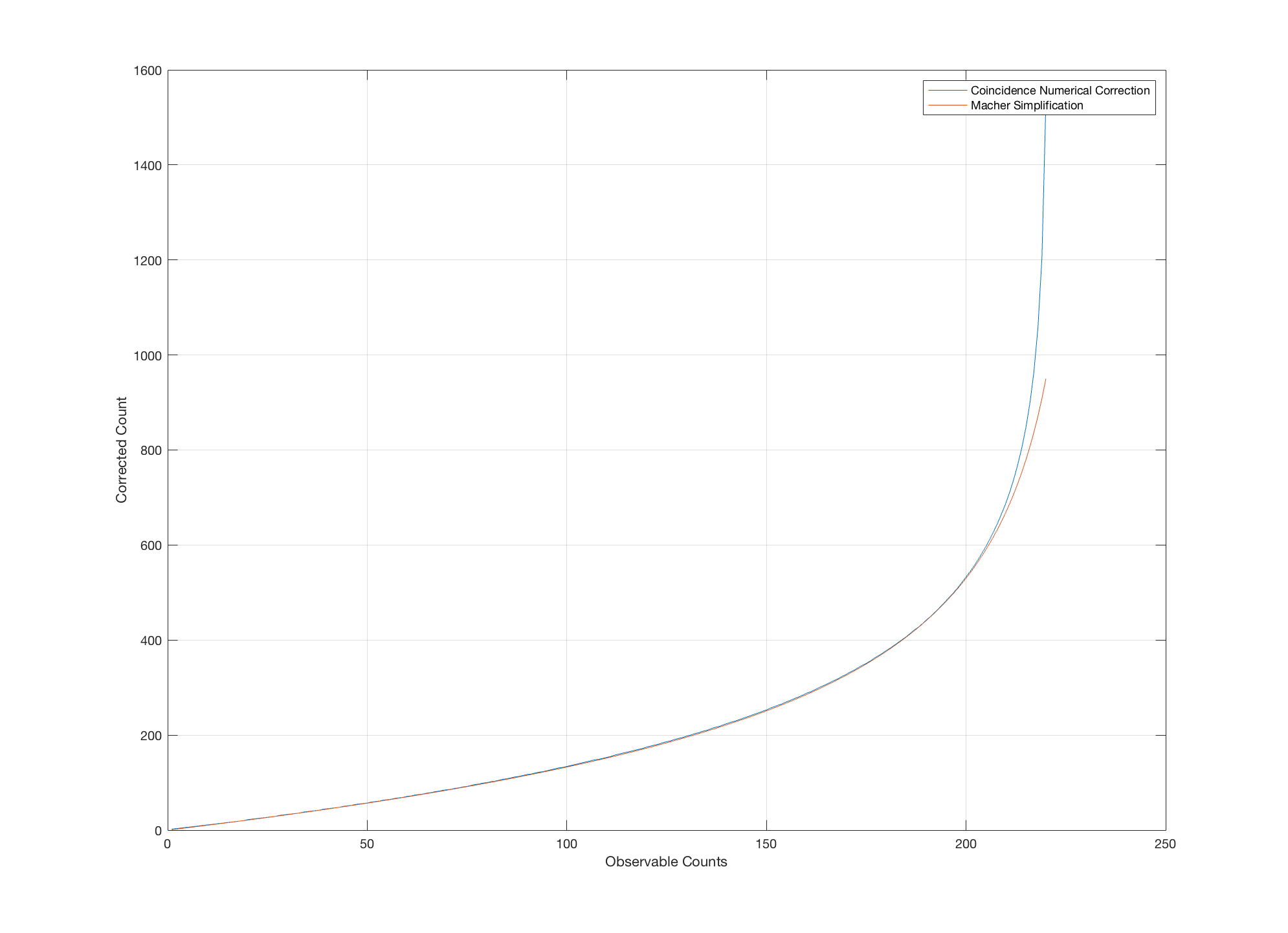
Coincidence Correction vs. Macher Simplification Plot for 220 Hole Head

A similar plot was made using the MATLAB model for a 400 hole head, by changing the N to 400:

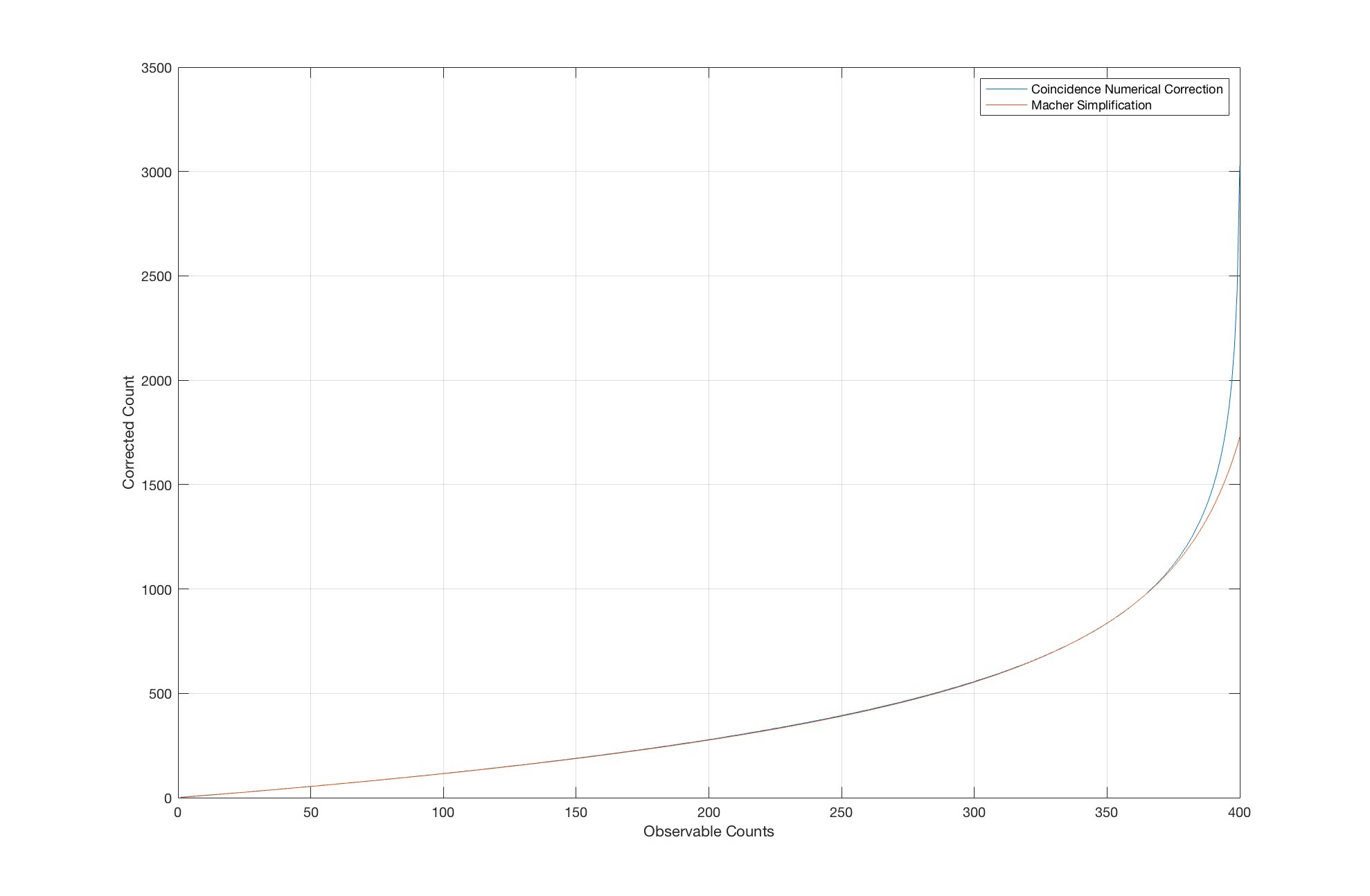
Coincidence Correction vs. Macher Simplification Plot for 400 Hole Head

As can be seen from the plots, at higher observable counts the results diverge. This is because the simplified equation is a best fit curve equation. In real life scenarios, equation(2)is sufficient, because it is extremely difficult to perform accurate observable counts of high numbers of colonies on a media/culture plate.

From the two plots, divergence occurs when the observable colony counts are above 90% of the number of holes in the sieve impaction head. In this situation, it could be considered an overloaded plate and lower volumes of air should be sampled to improve the reliability of the results.