Useful Formulas
Converting Milligrams per Liter to Parts per Million to Weight Percent
The conversions between milligrams per liter (mg/l), parts per million (ppm), and weight percent (wt%) can be confusing because the definitions are not always clearly spelled out.
Units of milligrams per liter (mg/l) are often used to report concentrations of dissolved constituents. Milligrams per liter is a ratio of mass or weight per volume. Parts per million (ppm), on the other hand, represents a ratio of weight per weight such as grams per million grams or pounds per million pounds. When the base fluid is fresh water, the value in ppm is numerically equal to the value reported in mg/l. The previous statement is true only because the specific gravity of the base fluid, water, is very close to 1.0. As long as the amount of dissolved solids is less than 1% or so, a liter of water weighs approximately 1,000 grams, which is equal to 1,000,000 milligrams.
Confusion can arise when the base fluid has a specific gravity substantially different than 1.0, as is the case for virtually all CBFs. In these cases, the conversion from mg/l to ppm must take into account the specific gravity of the base fluid.
To make the conversion, divide the value reported in mg/l by the specific gravity of the base fluid to convert to ppm.
EQUATION 22.
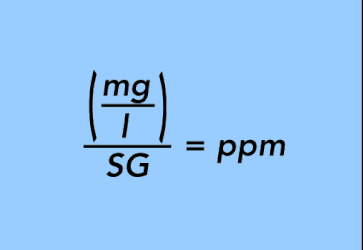
or going the other way,
EQUATION 23.
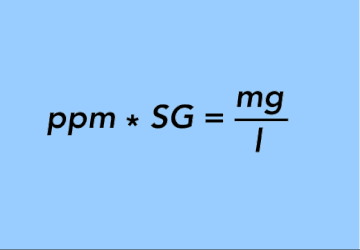
A third common unit of concentration is weight percent (wt%). Another way to think about weight percent is parts per hundred. By its definition, weight percent is a ratio of pounds of a substance per hundred pounds of total weight. It is a ratio of weight per weight and, as such, is similar to ppm. The easiest way to remember the conversion from weight percent to parts per million is that one tenth of a percent (0.1%) by weight is equal to 1,000 parts per million.
EQUATION 24.
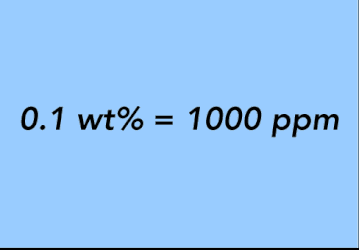
A quick conversion between the three different units of concentration can be made as long as the specific gravity is known.
Hole (Pipe, Tubing) Capacity
(in barrels per one linear foot, bbl/ft)
The first three equations are applicable to calculating internal volume and displacement for hole, pipe, or tubing using the inside diameter in inches.
EQUATION 25.
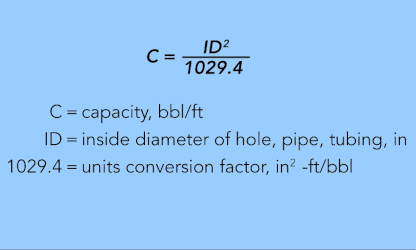
To determine the total volume of a hole, pipe, or tubing, multiply the value from Equation 25 by the length of the hole or pipe in feet.
EQUATION 26.

Annular Capacity
(in barrels per linear foot, bbl/ft)
The values derived using Equation 27 and Equation 28 are applicable to any combination of hole, casing, or liner on the outside and tubing or drill pipe on the inside.
EQUATION 27.

The capacity calculated using Equation 27 is the space for each foot of depth between casing and tubing or open hole and drill pipe.
Annular Volume
(volume between casing and tubing, bbl)
EQUATION 28.
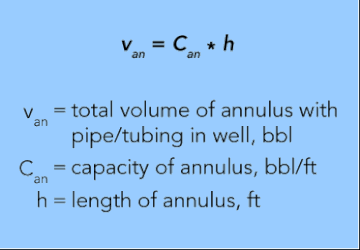
Velocity
(fluid flow rate, ft/min)
You use the same formula to determine velocity whether it is in a hole, pipe, or annulus. The input values are (1) the capacity in bbl/ft, gal/ft, or ft3/ft and (2) the pumping rate in bbl/min, gal/min, or ft3/min. Barrels, gallons, and cubic feet can be used as long as both terms (1) and (2) use the same unit of measurement.
EQUATION 29.

Pressure Differentials
Two columns of fluid exist, one in the annulus and one inside the tubing. They are in hydraulic connection, but substantial pressure differentials may exist between the two columns, especially when fluids are being changed or displaced from the hole.
Each length of annulus or tubing containing fluid with a different density is calculated separately. For example, if the annulus has three fluids with densities of d1, d2, and d3, respectively, and the true vertical lengths of coverage for each fluid are h1, h2, and h3, respectively, then the bottomhole pressure in the annulus (Pan) is:
EQUATION 30.
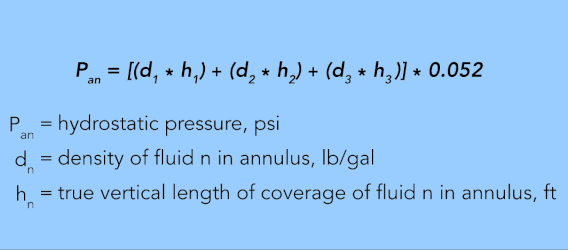
If the tubing of length (ht) is filled with a single fluid of density (d4) then Equation 30 simplifies to:
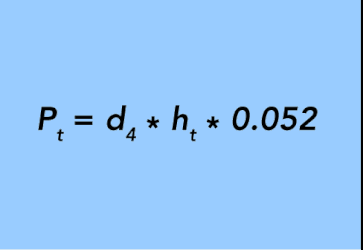
In this case, the pressure differential (Pdif) between the annulus and tubing (Pt) is the difference between the pressure exerted by the two columns of fluid:
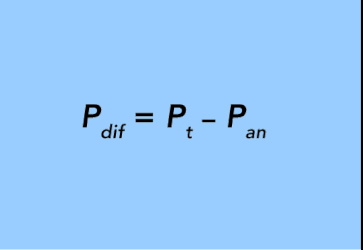
It is worth mentioning that the lengths of the two columns of fluid are normally equal:
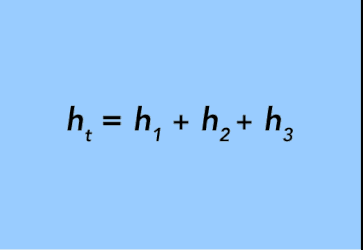
The preceding formulas will correctly calculate the volumes, quantities, and values they are designed to calculate. However, they are based on a perfect world. In the field, a 10.0 lb/gal fluid rarely, if ever, weighs exactly 10.0 lb/gal and fresh water rarely, if ever, weighs 8.34 lb/gal. Using the formulas to determine the volumes of various fluids or the quantity dry salt to use for a specific purpose is of great value. However, when applying this data to the actual exercise of adjusting fluid densities, approach the end point of this activity with caution. In other words, never add all of the required spike, dilution fluid, or dry salt without closely monitoring the progress of the fluid adjustment, especially as you near your end point. Adopting this approach will allow you to complete the adjustment with much greater accuracy.